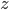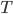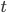I've been in an EarthCalc intellectual downswing for a few weeks -- just could not think of anything interesting. It is weird how we have these mental blocks at times. Fortunately, a week ago Saturday I went to the first local Data Visualization Hackathon and had the pleasure of working with some folks to explore the declining level of White Bear Lake.
I've discussed White Bear Lake a bit before in talking about aquifers and rate of change. This weekend at the hackathon we looked more explicitly at the lake level itself, rather than water level in aquifers nearby. White Bear Lake is striking because it has dropped many feet since 2003. That change is visible from space!! Look in particular at the upper left corner of the lake:
The video above simply takes images from the Landsat satellites from 1984 through 2012, and was made by Nate Bird at the data viz hackathon using images from Google. Check out Google's Earth Engine which gave us the idea.
I also put together a very quick graph of lake level (in blue) and precipitation (in green), with clashing scales. It's not the best visualization, but it gives some illustration of the fact that the USGS says that White Bear Lake's average levels used to roughly lag yearly precipitation by a few years, but since the early 2000s has been somewhat decoupled from yearly precipitation.
I have a few more illustrations to put up in the next post, as well as the worksheet. First, though, I'll ask you to think about how we should model the lake! White Bear Lake is very irregular in shape. Should we idealize it and model the surface as a rectangle? a circle? The shape of the bottom is also quite complex. Should we model the lake as a prism -- like a swimming pool -- or as a bowl? What are the right answers to these questions, and how would we be able to know if we answered right or wrong?