I've taught calculus now at several different college and universities. Calc is a funny class these days: students who have done quite well in high school math now often enter a linear algebra or multivariable calculus class directly, so students in calculus come from a variety of backgrounds but often did not have a good high school math experience. Often students in college calculus classes took the AP calculus offered in high school with varying results. A surprisingly high number of students I've seen in college calc did not even take precalculus in high school. This is generally a recipe for disaster.
During the fall and spring semesters I start every calculus section with a conversation about what calculus is good for and what other classes a student could take to fulfill requirements. I like to push statistics and math for liberal arts majors courses: statistics is becoming crucial to survival and innovation in a number of fields, from finance to medicine, and math for liberal arts majors classes often expose a student to graph theory, voting theory, and other useful techniques for looking at problems we all encounter in life. There is so much beautiful mathematics! Don't get stuck on calculus as the only way forward!
After that, it's time to start with review. I phrase it as a warm-up: here are things you will need to dredge out of your brain and reacquaint yourself with to be successful in calculus. First is the point-slope equation for a line.
The worksheet attached explores the change in atmospheric pressure as we increase in altitude from San Francisco to Denver to the peak of Mount Everest. In it, students develop a linear approximation for pressure in kilopascals from two data points (no use of derivatives), and then examine the validity of their approximation. Use this to explore:
- how to work through a word problem
- the point-slope equation for a line, introducing the idea of slope as rate of change
- critical thinking about models: comparing theoretical and actual results can point out weaknesses in a model!
When discussing this worksheet, remember that temperature, humidity, and weather patterns affect the pressure of our atmosphere as well. Some of the lowest pressure readings ever taken near the Earth's surface have been in the centers of hurricanes, for instance. In calculus we study "baby problems" so that we can eventually build up the techniques to model situations more accurately -- like scales before playing Beethoven.
Linear Functions -- Head in the Clouds Worksheet
How do you start out your calculus classes in the first few days? How much review do you do? Do you think all of your students are best served by calculus?
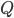 be the incoming solar radiation (insolation) and
be the incoming solar radiation (insolation) and  be albedo (percentage of sunlight the earth reflects) -- our "energy in" will be
be albedo (percentage of sunlight the earth reflects) -- our "energy in" will be 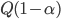 . Then we can use Boltzmann's black-body radiation to get "energy out" -- it's
. Then we can use Boltzmann's black-body radiation to get "energy out" -- it's  , where
, where 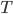 is our global average surface temperature in kelvins and
is our global average surface temperature in kelvins and 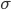 is Boltzmann's constant. So we get the equation
is Boltzmann's constant. So we get the equation