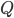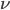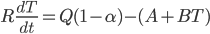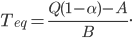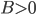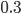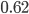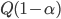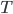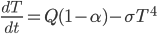I was on a math trip this week, so have been a bit delayed in posting. After four days of intensive pure math thought, I've returned to my little farm in the city, the minuscule plot that is my back yard. Today was spent doing math and picking cherries. The beans and peas are doing well, too; we've got peas planted where we used to grow tomatoes in an effort to increase the nitrogen content of the soil without applying fertilizer.
I have the luxury of not depending on my little garden for my primary food source. Instead, I buy food from farmers either at the farmer's market or at the grocery store. It is nice to live in the city and be able to take the bus to the opera, but it means I depend on others for agriculture. They use fertilizer and irrigate their land because farmers must do everything they can to control growing conditions for their crops.
Today is about sugar beet production. (I also looked into optimization of conditions for composting, but there are no equations I can find!) Sugar beets are a major crop across the US, particularly in North Dakota, Minnesota, and Idaho. We love sugar and want it in many foods (until we find it's killing us) and of course farmers want to optimize their yields. Sugar beets are interesting because simply adding more nutrients to the soil can be counterproductive: you don't want the biggest sugar beets, you want the sweetest ones! Too little nitrogen means yellow leaves and poor growth. Too much nitrogen means impurities in your beets and reduced sucrose, or at worst killing your seedlings (source). It's the Goldilocks question.
An older report on how nitrogen levels affect recoverable sugar yields has some very nice equations. G.L. Malzer and Greg Buzicky looked at many variables and came up with several equations that predicted recoverable sugar yield pretty well, all in terms of the soil's nitrate-nitrogen content. And they're quadratic! This is a nice way to do a pretty easy optimization exercise with applications to something... sweet!
The first page is all about finding the optimum recoverable sugar yields given different levels of nitrate-nitrogen in the soil. The second page mixes in some experimentation and treats a two-variable function, foreshadowing multivariable calculus techniques. Including discussion of multivariable functions in a first-semester calculus course is a really cool idea that deserves more attention -- it does not disturb students, but only people who have a set idea of what one "should" learn in first-semester calculus. The third page asks students to use the first and second derivative tests to prove the results they've already produced, and asks them to think about the applicability of the Extreme Value Theorem. As in many situation, physical constraints could lead to a closed-interval phrasing of the problem, although it's not necessary mathematically. Provoke an argument!
Optimization: Sugar Beets
Agriculture is often ignored in calculus and STEM classes, as it's not so sexy these days. Universities like the University of Minnesota and Cornell have big ag programs, though, and they're hugely important. You sure can't be a vegan or vegetarian in the north without the products of modern agriculture!
I've learned a lot from my ag students and they need to deal with optimization often: they need to optimize nutrient composition in animal feed, optimize nutrient composition of fertilizers for soybean growth, optimize temperature for dry-matter intake of chickens, and of course look at the economics of all the above. Their decisions impact the diets, waterways, air quality, climate, and fuel prices of city-dwellers. Don't forget the ag, even if you live in LA.