We instructors of calculus know that linear models aren't everything, even though linearization is in some sense the point of the differential calculus. Since the first week of many calculus courses begins with a precalc review including power functions, I'll just move smoothly along to a power function model for atmospheric pressure! (Don't worry: we'll get to lynx trapping in the Yukon for a trig review activity in a day or two -- not everything is about physics or the atmosphere.)
It's always important to remind students about the difference between power functions and exponential functions, not least because they've got different differentiation rules. One nice way to look at power functions and exponential functions is by looking at growth -- we know that 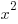 and
and 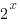 grow at very different rates. But everyone does that... and I was having fun with atmospheric pressure! This worksheet has a very funky power -- 1/0.19... -- and might be a good way to acquaint students with the messiness of real-life models. I will return to this topic when we get to derivative and integrals, too, because this equation is actually fairly easy to derive.
grow at very different rates. But everyone does that... and I was having fun with atmospheric pressure! This worksheet has a very funky power -- 1/0.19... -- and might be a good way to acquaint students with the messiness of real-life models. I will return to this topic when we get to derivative and integrals, too, because this equation is actually fairly easy to derive.
The worksheet below tries to foreshadow the idea of the derivative fairly heavily. It asks about
- composition of functions,
- intervals of increase and decrease, and
- slope of the tangent line.
As usual, I try to incorporate a bit of writing and thinking about the meaning of a model as well. There's definitely room for discussion around these worksheets.
In addition, you might notice that there's a bit of tedious calculation at the beginning. Why would an enlightened modern instructor do that? I like to give these worksheets to students in groups. At the beginning of the semester I always give a student survey asking about past math experience, major, problems or gifts I should know about, outside interests, favorite dessert, favorite color. In the first few weeks of class I use this to arrange student groups and ask them to figure out how I've grouped them (by major, dessert, color, last name...!). Giving them just a bit more tedious calculation than most people would enjoy gives me a chance to encourage and incentivize conversation within groups even more.
This week's worksheet: atmospheric pressure as a power function!
A better model: power function
There's also a natural place to discuss solving for the inverse function here, and I might add a worksheet about that soon too.
Do you use group work or worksheets with students? Why or why not? What kinds of constraints do you have to deal with in considering group work?
