We return to naproxen (sold under the brand name Aleve). Naproxen is my "drug of choice" for these worksheets because it apparently occurs in a lot of our waterways and its decay is pretty well understood. Last time we discussed naproxen in particular, we looked at a function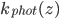 
that gives the rate of photolysis for naproxen at a depth 
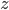, the rate at which the substance breaks down in the presence of sunlight. There are a few different ways that substances like naproxen, ciprofloxacin (an antibiotic), cocaine, or bisphenol-A get taken out of waterways: breakdown in sunlight, breakdown by organic processes, or sedimentation. Naproxen breaks down easily in sunlight but it doesn't like to be filtered by sand or settle out into sediment even when the water is treated with ferric sulfate to make coagulation happen.
The linked abstract is for a paper about a pilot-scale drinking water purification plant, looking at how water from the River Vantaa could be used for drinking water if the groundwater source for Helsinki, Finland, were to be rendered unusable. Remember that groundwater usage is increasing enormously across the world, and so our nice clean aquifers are overtaxed in many locations. We should not waste so much water (agriculture and lawns, folks!) but will also need to learn a lot about how surface water can be purified so that we can drink it again.
The worksheet below has a mix of derivative and rate of change questions. It asks about some derivatives that require the chain rule (quotient rule and exponential function rule combined) and it also asks students, at the end, to switch variables and look at how the rate of photolysis changes as turbidity changes. After every heavy rain a lot of sediment enters a river and then settles out over time. Development and construction can also change turbidity substantially: digging up a lot of trees and plants to expose dirt allows a lot of that dirt to run off. Agriculture also has its role, as during the planting season fields can be vulnerable to erosion and run-off.
Chain Rule: Photolysis of Naproxen
If you're in a position to work with a science teacher or run experiments yourself, I found a fun page on experiments with turbidity appropriate to junior to senior high school students (and what college student wouldn't mind playing with mud, really?). This could make a cool big brother/big sister activity: high school seniors do the math and the freshmen or junior high students do some experiments on turbidity. In addition, there's a World Water Monitoring project and day (September 18) that you could join.
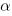or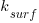 
, though they'd prefer to!
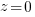, always a somewhat challenging concept for students. The limit as z goes to infinity can be done with limit rules.