Some instructors (like me!) like to foreshadow the ideas of concavity early in the semester. When I talk about rate of change, average and instantaneous, I like to throw out some discussion of the rate of change of the rate of change. This is a language puzzle for many students -- they may see that a function is increasing but need to think harder about whether it is increasingly increasing or decreasingly increasing. What does that all mean, anyway?! It's a great time to discuss precise mathematical language, communication skills, and the usefulness of equations. It is easy to be precise when symbolically indicating that a function is concave up, but our English language can obscure meaning here. Politicians certainly take advantage of this when discussing the decreased rate of growth in the budget or slowing the rate of budget cuts for social programs!
(Any examples a reader would like to publicize here? I know I've heard some great political lines like this but I cannot find a citation...)
This worksheet goes back to the air pressure activity introduced earlier. It is a fairly straightforward exercise in
- computing average rates of change,
- plotting secant lines, and
- taking a first pass at the concept of concavity.
Because it's straightforwardly computational rather than deeply conceptual, use this for a moment in class when you want students to work through the ideas but also want to give them a little mental break. It's a good time for getting a drink of water or chatting a bit about how things are going. Sometimes students need some computation and a stretch, as the ability to concentrate on mathematics for more than twenty minutes at a time takes development through repeated practice.
I've been working on a post about interpretation of story problems and graphs, so that will probably make an appearance next week. It's also time to go toward derivative rules and derivative graphing. Good old-fashioned non-applied explanations of the derivative at a point and the derivative as a function are up to you, as I find students need a purely mathematical or formal explanation before applications. We'll revisit lynx and naproxen and hopefully add another story to the mix!

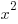 and
and 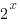 grow at very different rates. But everyone does that... and I was having fun with atmospheric pressure! This worksheet has a very funky power -- 1/0.19... -- and might be a good way to acquaint students with the messiness of real-life models. I will return to this topic when we get to derivative and integrals, too, because this equation is actually fairly easy to derive.
grow at very different rates. But everyone does that... and I was having fun with atmospheric pressure! This worksheet has a very funky power -- 1/0.19... -- and might be a good way to acquaint students with the messiness of real-life models. I will return to this topic when we get to derivative and integrals, too, because this equation is actually fairly easy to derive.