How's that for a sensational headline?
This post is a bit late because of units. I got some wonderful data on personal care products and pharmaceuticals in wastewater from a reader: several pages of information on what's going into and coming out of the wastewater treatment plants in Silverthorne, Dillon, and Frisco, Colorado. These three wastewater treatment plants treat water from homes all around the Dillon Reservoir and then put treated water out into the reservoir itself, which eventually provides drinking water to Denver. They're doing the same great work wastewater treatment plants around the US and the world are doing: taking our extra coffee, our dishwater, and our waste and putting out pretty clean water!
The study I'm looking at used six trips over three years to look at influent (incoming water) and effluent (outgoing water) at these wastewater treatment sites. The authors used grab samples -- quick samples taken at one time, rather than samples taken at specific repeated times or water sampled throughout the day -- to get a cost effective test of water quality. Now, water spends some time in the wastewater treatment plant (this is called resonance time or residence time) and so a grab sample will not reflect what happens to a particular batch of water that goes in -- if it takes three hours, for instance, for water to get processed, but you take samples of influent and effluent ten minutes apart, you're measuring different parts of the stream. That will explain a bit of the weirdness we encounter on page three of the worksheet. Naproxen and cocaine are very effectively removed from water by current treatments, but hydrocodone is not and so it looks like more is coming out of the treatment plant than is going in!
Back to units, though: I wanted to do a worksheet using Riemann sums to estimate quantities of pharmaceuticals in the water supply, but all my data is in nanograms per liter and I wanted to look at it against time rather than volume. So I had to figure out how to get nanograms or grams per day, and that involved finding out how much water each wastewater treatment plant processed. Not totally easy. But I did manage it roughly. I found that in 2002-2004 the Snake River Wastewater Treatment plant was processing about 27% of its official capacity of 2.6 million gallons per day and used that figure. The Joint Sewer Authority (JSA) plant in Silverthorne says in its financial statement that it processes four million gallons/day. (I'd like to check those numbers, and have an email out to the Snake River folks.) Turn those into liters, and we can get nanograms per day. But those numbers are ugly decimals, so let's talk about grams per day!
I made two Google spreadsheets, one with data for students to use and one with the answers (for you and me, on the solutions page). This activity is best as a computer activity, I think, although if students have graph paper available I did provide the data on the worksheet pdf and it would not be toooo onerous to do the Riemann sums by hand. Up to you to manage the discussion about drugs.
Numerical Integration: Naproxen, Hydrocodone, Cocaine
Student version of spreadsheet
I will change the numbers if the Snake River folks respond with more up-to-date information about how much water they are treating per day.
Anyhow, this worksheet deals with using Riemann sums to roughly estimate a quantity (net amount) given a rate. If you choose to make it a computer activity, it's pretty straightforward to answer all the questions in a concentrated class group-work session. If you decide to do this only on paper, you might choose not to deal with all three chemicals -- it might take more time than is appropriate for an in-class activity. Each chemical is on a different page so mix and match!

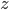 . Then a reasonable simplification of the heat equation tells us that temperature
. Then a reasonable simplification of the heat equation tells us that temperature 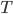 depends on depth
depends on depth 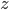 and time
and time 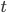 in the following way:
in the following way: