Arctic Ice 2, Wikimedia Commons
Let's get to it! Today's worksheet is about deriving Stefan's equation. In 1891 Josef Stefan came up with a simple model for the thickness of sea ice, using thermodynamic reasoning and the data from British and German Arctic explorers. We, too, can trace through the thermodynamic reasoning. I found it harder to find straightforward sea ice thickness data for areas without snow.
To get technical here, we can start with the heat equation and some boundary conditions on the temperature at the top of the slab of sea ice and the bottom of the slab of sea ice. It's easiest to assume, though, that temperature in the ice sheet depends on vertical depth from the top of the ice sheet -- not so much on horizontal coordinates. That means we can use a model with one spatial dimension, depth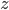 
. Then a reasonable simplification of the heat equation tells us that temperature 
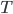depends on depth 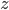and time 
in the following way:
