Jim Walsh from Oberlin opened today by talking about greenhouse gases and energy balance equations. His slides are online -- check them out for all the great pictures I have not included!
First big conceptual point: global climate is determined by the energy in minus the energy out. Since energy in is basically the insolation (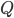
-- incoming solar radiation) that is not reflected (multiply by 1-albedo) and energy out is OLR (outgoing longwave radiation) these are the three factors to look at -- change in insolation, albedo, or OLR. If these are changed by our human activities (or anything else!) climate will change.
Here Jim talked about the Earth Radiation Budget Experiment briefly.
Energy balance and greenhouse gases
Radiation is characterized by its direction of propagation and frequency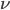 
. We need to know about electromagnetic spectrum, and for climatology (look at Pierrehumbert's book, p137) we need infrared through ultraviolet.
Need some math concepts to construct some integrals. We know what radians are -- the arc length on a unit circle cut out by an angle whose point is at the center of the circle. For the surface of the earth, we need steradians. "The measure in steradians of a solid angle made by a collection of rays emanating from a point P is the area of the patch of the unit sphere centered on P which the rays intersect. "
Since we’re interested in the radiation emitted by a piece of the surface of the earth we’re looking at solid angle differentials.
Energy of radiation is measured by its intensity or radiance I. Given
- Frequency increment
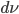
- Increment of area
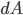
- Solid angle incremend
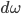
- Time increment
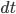
The amount of corresponding radiant energy is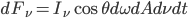 
.
Folks often think instead about energy per unit frequency per unit area per unit time. Different units.
Integrating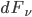 
we can get the spectral flux density; this expression depends on frequency. This spectral flux density is 
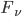. Integrate that over all frequencies and get flux density 
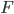, with units 
.
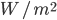Black body radiation is simple. Planck’s Function depends only on 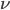(frequency) and temperature, not angle. So for a given frequency , 
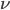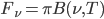. This 
is too complicated for me to type 🙂 so take a look at Jim's slides!
To get total flux density integrate $F_{\nu}$ over all 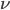and get 
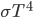. Stefan-Boltzmann. We can do this integral. Related to Euler’s work on Riemann zeta function. Interesting integral through u-substitution. I'm going to work through this later!
We can make certain assumptions to make an "ideal" example situation:
- Albedo spatially uniform
- Planet radiates like a perfect blackbody
- Planet’s atmosphere is perfectly transparent to the electromagnetic energy emitted by the surface
- Planet’s radius is a, star’s temp is
, 
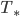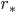is star’s radius, r is distance to star
Total flux impinging on planet is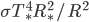 
, the solar constant 
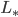. Energy absorption is 
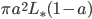. Energy loss is 
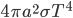. Equilibrate:
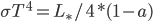and solve for 
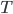. What's the point? We find that the planet loses energy at a lower wavenumber than it gets it in from the star.
Ok, fine. We know something about the wavelengths/wavenumbers that the planet is emitting. What do we do with that? Getting closer to greenhouse gases...
Flux absorption: Beer’s Law. Absorption is proportional to the flux F times the mass of the absorber (greenhouse gas, eventually) along the path. So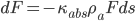 
. 
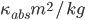is absorption coefficient, which is a function of 
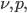and 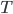, where 
is pressure, and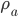 
is the density of the absorber.
We’re assuming that there’s no scattering, and assuming that atmosperic properties are functions only of the vertical coordinates. Look at the figures here, too. Notice that if kappa and rho were constants, this would look like exponential decay!
Adding greenhouse gases dramatically decreases amount of OLR. CO2 is particularly good at absorbing OLR. Look at the picture of the CO2 absorption spectrum — almost complete absorption in wavelengths that earth emits. Notice also that H2O complements the CO2 absorption spectrum -- humidity and CO2 absorb different parts of our outgoing longwave radiation.
Notice the dips in outgoing radiation exactly at the absorption ranges of H2O, CO2, O3, and H2O. This absorption means temperatures increase on earth and then the Planck curve must move over.
A+BT -- a math model?
Jim then moved to A+BT: logarithmic dependence of OLR on CO2. Several papers cited. Marshal, Walker, and Kuhn did something very mysterious but came up with log functions; Caldeira, Kasting came up with cubic functions in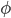 
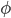, = ln pCO2.
Mathematically what can we figure out? Look at equilibrium solution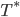 
. As A increases, 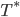decreases. Look at place where ice line 
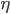doesn't move, and then solve for A. Can find 
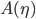. Then plot bifurcation plot. I'm going to have to think about this one... don't quite understand the bifurcation diagram yet!
Last topic -- Jormungand climate model: geological and paleomagnetic evidence indicate that during at least neoproterozoic glacial periods continental ice sheets flowed into the ocean near the equator! So almost our whole earth was covered in ice. That means there was positive ice-albedo feedback. Snowball earth hypothesis. However, there's an alternative theory: thin strip of open ocean about the equator with organisms in it that ate stuff. Jim then shows a modification of the model and some graphs coming from the numerical solutions, with more bifurcation diagrams.