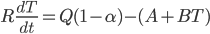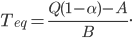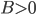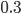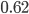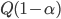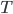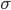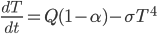Backing away from the sensational headlines of last week, here's something a bit more relaxing. Our atmosphere is leaking away into space and maybe someday eventually we won't have one anymore. How's that?
Alright. I exaggerate a bit here -- the force of gravity is enough to keep nitrogen and oxygen around, as well as lovely greenhouse gases like carbon dioxide and methane. These are heavy molecules! Hydrogen, on the other hand, is really light. It reaches escape velocity fairly easily, especially at the outer reaches of the earth's atmosphere.
For a more nuanced look at atmospheric escape, check out the Scientific American article. I'm linking to an author's website because I can't get this article at the Scientific American site even via Cornell's library.
Today's worksheet is another longish one. I might consider splitting it up. The first two pages guide the student through a derivation of escape velocity using the chain rule, integration, and limits. It's one of those activities that dredges up everything a student had to learn all semester, yet in the end none of the integration or limits are that hard. The last page (the third) asks some very concrete questions about the escape velocity for hydrogen molecules, relating this velocity to temperature. "Is it hot enough for hydrogen to escape?" is the main question.
I have to confess that I spent all day traveling to a math conference and I'm a bit underslept. As I went through my calculations I realized that hydrogen could escape from anywhere in the earth's atmosphere, and this really alarmed me! We are all going to perish! until I realized that indeed that's the case, and that's why we basically have no hydrogen in our atmosphere. It's ok. Can't breathe that stuff anyway.
Let me know if you use this worksheet and whether you think it would be better broken up into parts. I like the surprising results, and I like the fact that it brings together the chain rule, integration, and limits. It would be fun to extend it and talk about the moon's lack of atmosphere and Venus's crushing anvil of an atmosphere. We sometimes take for granted our Goldilocks world...